版权声明,此安装案例来源公众号:铁道科学与工程学报.敬海泉:半漂浮体系钢管混凝土拱桥黏滞阻尼器减震研究.https://mp.weixin.qq.com/s/4FundKm2JjD_8uTlHHj0BQ
文章以某计算跨径252米的中承式钢管混凝土拱桥为例,采用动力时程分析方法研究了半漂浮式主梁钢管混凝土拱桥中黏滞阻尼器参数的选取方法,对比分析设置黏滞阻尼器前后桥梁结构的地震响应。结果表明:设置黏滞阻尼器能显著减小半漂浮体系主梁的地震位移响应,同时也导致拱顶纵桥向位移有所增加,对拱肋各关键位置处轴力、剪力、弯矩响应的影响规律不尽相同,对黏滞阻尼器位置处的拱肋局部弯矩响应影响较大。该研究成果可对采用半漂浮式主梁的钢管混凝土拱桥的减震设计提供参考。
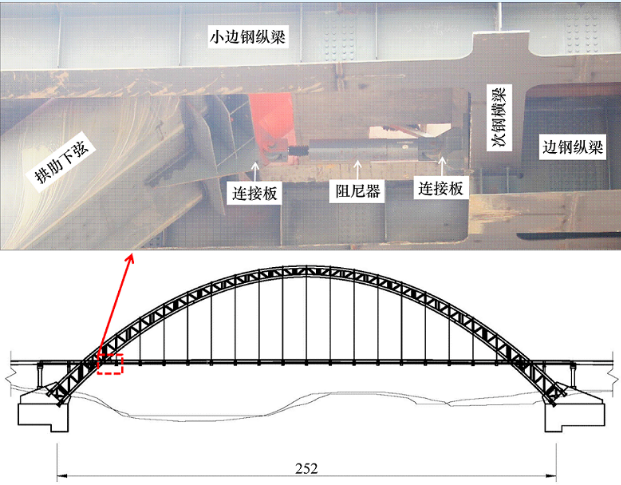
图1 计算跨径252米的中承式钢管混凝土拱桥立面布置与黏滞阻尼器位置图

图2 桥梁空间有限元模型
01 研究背景
钢管混凝土拱桥在全国得到了广泛应用,其主梁近年来向连续化和轻型化方向发展,为释放温差变形引起的结构内力,大跨钢管混凝土拱桥主梁宜采用半漂浮体系,但半漂浮体系主梁在地震作用下的水平位移较大,应设置黏滞阻尼器控制桥面梁在地震作用下的响应。本文以某计算跨径252 米的半漂浮体系中承式钢管混凝土拱桥为工程背景,采用非线性动力时程分析法研究了黏滞阻尼器在该类桥中的参数选取方法与减震效果。
02 主要内容
# 自振特性分析
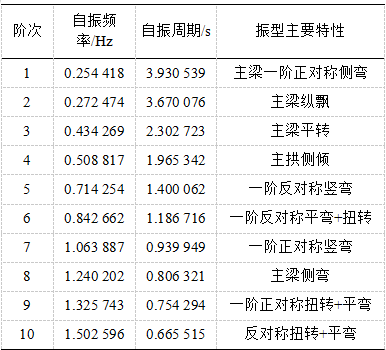
采用多重Ritz向量法求解设置黏滞阻尼器前的桥梁结构动力特性,桥梁结构前十阶结构自振频率和振型主要特性如表1所示。前三阶振型均为拱桥主梁的振动,这是由于采用半漂浮体式主梁的钢管混凝土拱桥对主梁的约束较小,因而在自振特性分析中阶次出现的较早,其中第2阶振型为主梁纵飘,振型参与质量达到49%,对纵向振动贡献较大,起主导作用,可以预见其在地震中的响应对桥梁整体结构的影响也较大。
表1 桥梁结构动力特性
# 黏滞阻尼器参数选取研究
对中承式钢管混凝土拱桥而言,有两个地方可供选择作为阻尼器安装位置,一是在交界墩与主梁梁端之间,二是拱肋与主梁之间。一般而言交界墩较高,纵桥向刚度不够大,在地震作用下可能与桥面主梁一起沿纵桥向振动,不能达到减震的目的,而拱肋刚度大,在地震作用下纵桥向位移小,故最终选择在拱肋与主梁之间设置纵桥向黏滞阻尼器来减震。选定与桥址处工程场地相符的地震波加速度记录,参考已经在工程中实际使用的黏滞阻尼器参数,将黏滞阻尼器阻尼系数试算范围取为500~4 000,阻尼指数ξ试算范围取为0.2,0.25,0.3以及0.35进行参数分析,计算结果汇总如图3和图4所示。
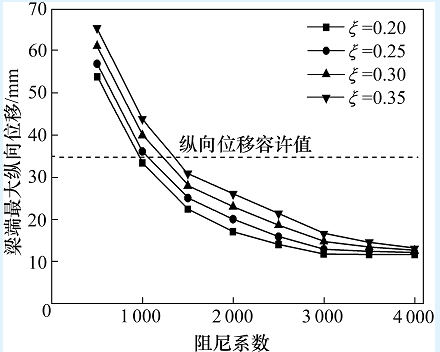
图3 阻尼系数与阻尼指数对梁端纵向位移响应的影响
从图3可以看出,梁端最大纵向位移响应随着阻尼系数与阻尼指数的变化而变化,对相同的阻尼指数,梁端最大纵向位移响应随着阻尼系数的增大呈非线性减小,并收敛于约11.7 mm,这是由于阻尼系数很大时,接近主梁与拱肋固结的情形,故梁端最大纵向位移响应不再随阻尼系数而变化。对相同的阻尼系数,梁端最大纵向位移响应随着阻尼指数的增大而增大。图中虚线所示为梁端纵向位移容许值,虚线下方各曲线取值为满足纵向位移要求的阻尼系数与阻尼指数。
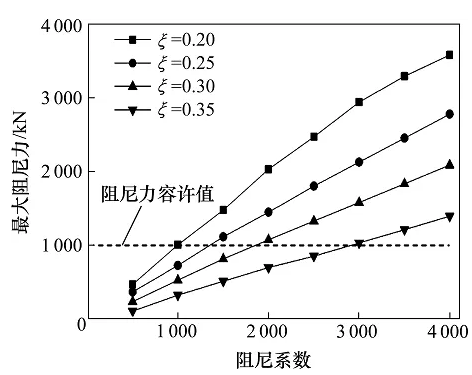
图4 阻尼系数与阻尼指数对阻尼力的影响
从图4可以看出,最大阻尼力响应也随着阻尼系数与阻尼指数的变化而变化,对相同的阻尼指数,最大阻尼力响应随着阻尼系数的增大基本呈线性增大,对相同的阻尼系数,最大阻尼力响应随着阻尼指数的增大而减小。图中虚线所示为阻尼力容许值,虚线下方各曲线取值为满足阻尼力要求的阻尼系数与阻尼指数。
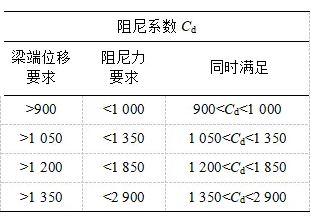
显然,同时满足梁端纵向位移要求与最大阻尼力要求的阻尼系数与阻尼指数为两图中虚线下方各参数的交集,如表2所示。此外,黏滞阻尼器滞回曲线面积越大耗能能力越强,应选择滞回曲线尽量饱满的黏滞阻尼器,同时结合黏滞阻尼器生产商的产品规格序列,最终选定用于该桥梁的黏滞阻尼器指数ξ=0.3,阻尼系数Cd=1400。
表2 阻尼系数与阻尼指数选取
# 黏滞阻尼器减震效果分析
通过计算分析,可以得到在地震作用下阻尼器设置前后关键部位(本文选取梁端纵向位移、拱顶纵向与竖向位移)的位移时程,图5和图6示出了设置阻尼器前后,地震作用下梁端纵向位移与拱顶纵桥向位移响应时程对比。设置黏滞阻尼器前,梁端最大纵向位移响应约99.2 mm,远超过梁端纵向位移容许值35 mm,设置阻尼器以后,梁端纵向位移响应最大值为29.3 mm,小于梁端容许位移限值,梁端纵向位移响应减少了约70%,这非常有利于避免地震作用下伸缩缝破坏与梁端碰撞。拱顶纵向位移增大了29%,这是由于拱肋承受了阻尼器传递过来的主梁地震力所致,由于拱肋刚度较大,拱顶位移响应的绝对值变化并不大。
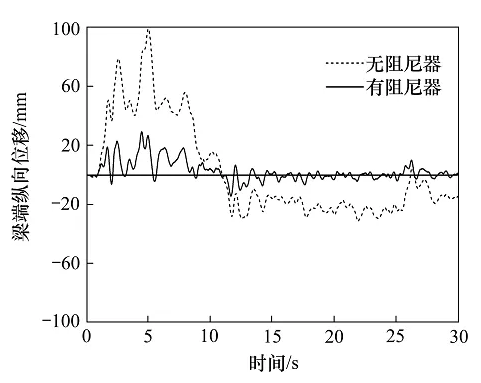
图5 设置阻尼器前后梁端纵向位移时程比较
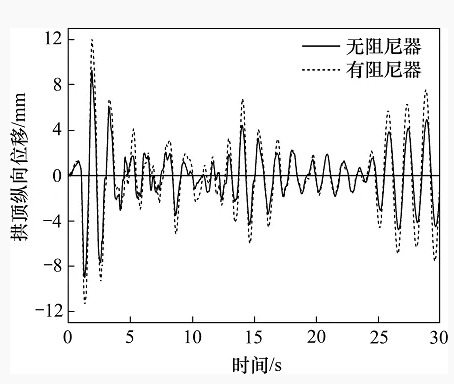
图6 设置阻尼器前后拱顶纵向位移时程比较
同理,通过动力时程分析可以得到阻尼器阻尼力以及阻尼器设置前后的拱肋关键部位(本文选取拱脚、阻尼器位置处、L/4处与拱顶)的内力响应时程曲线。计算得到地震过程中的最大阻尼力为745 kN,小于容许值1 000 kN,满足阻尼器选取要求。图7示出了设置黏滞阻尼器前后,地震作用下阻尼器位置处拱肋下弦弯矩响应时程对比。由于控制设计的往往是地震内力响应最大值,因此提取地震内力响应时程中的最大值(轴力以拉为正,以压为负,地震内力与恒载内力组合时,地震轴压力更为不利,故仅比较轴压力),汇总如表3所示。设置黏滞阻尼器以后,地震作用下,在阻尼器位置以下拱肋轴压力有所增加(约4%~35%),而阻尼器位置以上拱肋轴压力有所减少(约3%~7%),其中,拱脚上弦轴力增加约35%,拱顶上弦轴力减少约5%。除拱脚与L/4(L为跨径)处上弦外,其他各处剪力响应增大了15%~30%。各处弯矩响应均有所增大,设置阻尼器处拱肋下弦弯矩增大了122%,其他各处弯矩响应增大了0%~37%,这说明设置黏滞阻尼器对阻尼器处拱肋弯矩响应的影响大于其他各处拱肋,但由于拱肋刚度较大,经计算,设置阻尼器情况下,地震引起的阻尼器处拱肋下弦弯曲应力仅为4.88 MPa,应力绝对值仍较小。
表3 关键截面内力最大响应比较
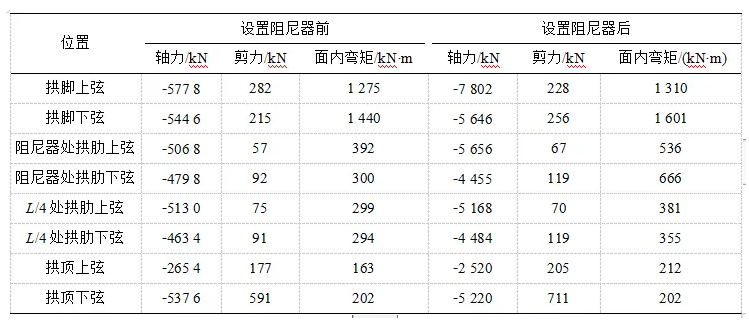
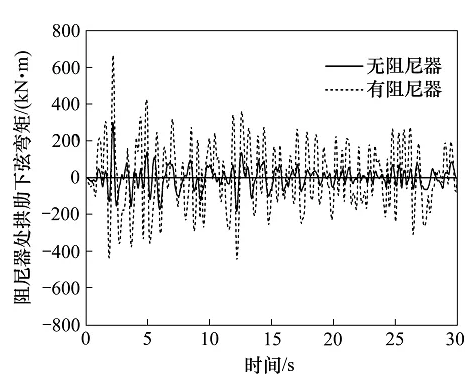
图7 设置阻尼器前后阻尼器位置处拱肋下弦弯矩时程
03 结论
1) 以梁端容许位移与阻尼器连接件所能承受的最大阻尼力作为控制因素,通过参数分析得到满足减震需求的黏滞阻尼器参数的方法是可取的。
2) 设置合适的阻尼器以后,能显著减小梁端位移(工程实例减小约70%),同时也导致拱顶纵向位移有所增加,但由于拱肋整体刚度较大,拱顶纵向位移响应绝对值依然较小,仅12.0 mm。
3) 设置阻尼器以后,对拱肋各关键位置处的轴力、剪力、弯矩响应的影响规律不尽相同。








